Question 1. Match the columns in the following table and explain them:

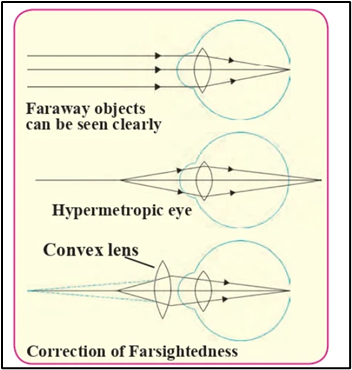
1. Farsightedness, also known as hypermetropia, is a vision condition where distant objects are seen clearly, but nearby objects appear blurry. In hypermetropia, the image of a close object falls behind the retina instead of directly on it. There are several possible causes of hypermetropia. Firstly, the curvature of the cornea and eye lens decreases, leading to a reduction in the eye lens’ converging power. Secondly, the distance between the eye lens and retina decreases in comparison to a normal eye, causing the eye lens’ focal length to become very large due to the flattening of the eyeball.

Farsightedness

2. Presbyopia:

Presbyopia is a vision problem that makes it challenging for older individuals to see nearby objects clearly and comfortably without glasses. This occurs because the eye’s ability to adjust decreases with age, causing the muscles near the lens to lose their capacity to change the lens’s focal length. As a result, the eye’s near point shifts farther away, leading to the need for correction with a convex lens of the right power. This lens converges light rays before they reach the eye lens, allowing the eye lens to focus the image on the retina.

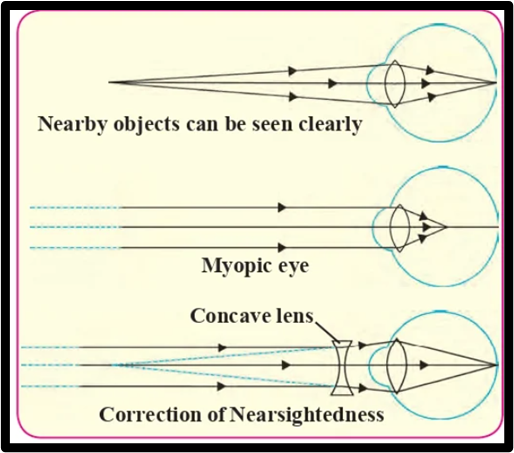
1. Near sightedness, also known as myopia, is a vision condition where objects that are close can be seen clearly, but distant objects appear blurry because the image is focused in front of the retina instead of on it.

Causes of myopia may include:

1) Increased curvature of the cornea and eye lens, leading to difficulty for the lens muscles to relax, resulting in a sustained strong converging power of the lens.

2) Elongation of the eyeball, causing an increase in the distance between the eye lens and the retina. Myopia can be corrected by using a suitable concave lens. The concave lens diverges light rays before they reach the eye lens. A concave lens with the appropriate focal length is selected to achieve the necessary divergence. As a result, the image forms on the retina after the converging action of the eye lens.

Near Sightedness

Question 2. Draw a figure explaining various terms related to a lens.

Answer: 

(1) The centres of the spheres forming the surfaces of a lens are known as the centres of curvature of the lens. A lens has two centres of curvature, C1 and C2, for its two spherical surfaces.

(2) The radii of the spheres contributing to the lens surfaces are referred to as the radii of curvature of the lens.

(3) The principal axis of the lens is the imaginary straight line that passes through the two centres of curvature of the lens.

(4) The optical centre (O) of the lens is the point inside the lens on the principal axis through which light rays pass without altering their path.

(5) The principal focus (F) of a lens is the point on the principal axis where light rays parallel to the principal axis converge or diverge after refraction. A lens has two principal foci, F1 and F2. (6) The focal length (f) of a lens is the distance between the optical center and the principal focus of the lens

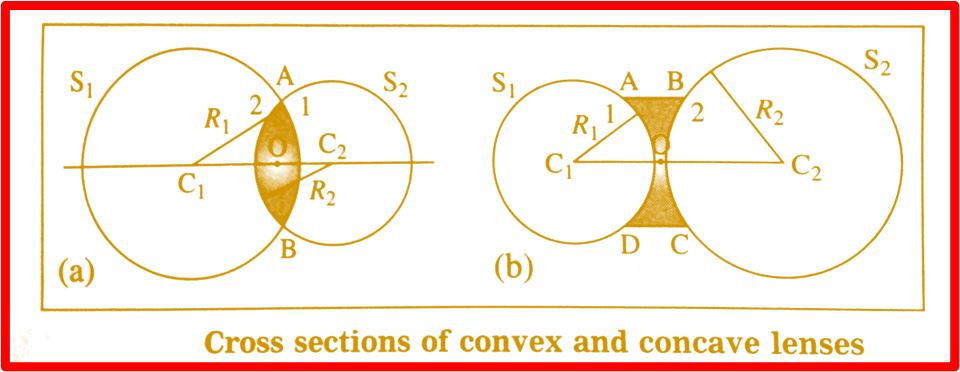
C1, C2 represent the centres of curvature, while R1 and R2 indicate the radii of curvature. O denotes the optical centre. Figure displays the cross sections of convex and concave lenses in segments (a) and (b). Surface 1 belongs to sphere S1, and surface 2 is associated with sphere S2.

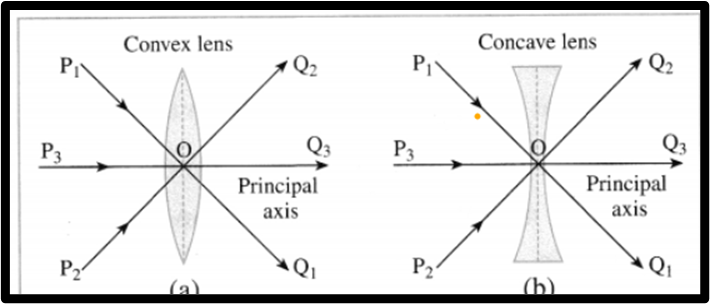
Optical centre of lens

P1, P2, P3: Incident rays of light,

Q1, Q2, Q3: Refracted rays of light, O: Optical centre

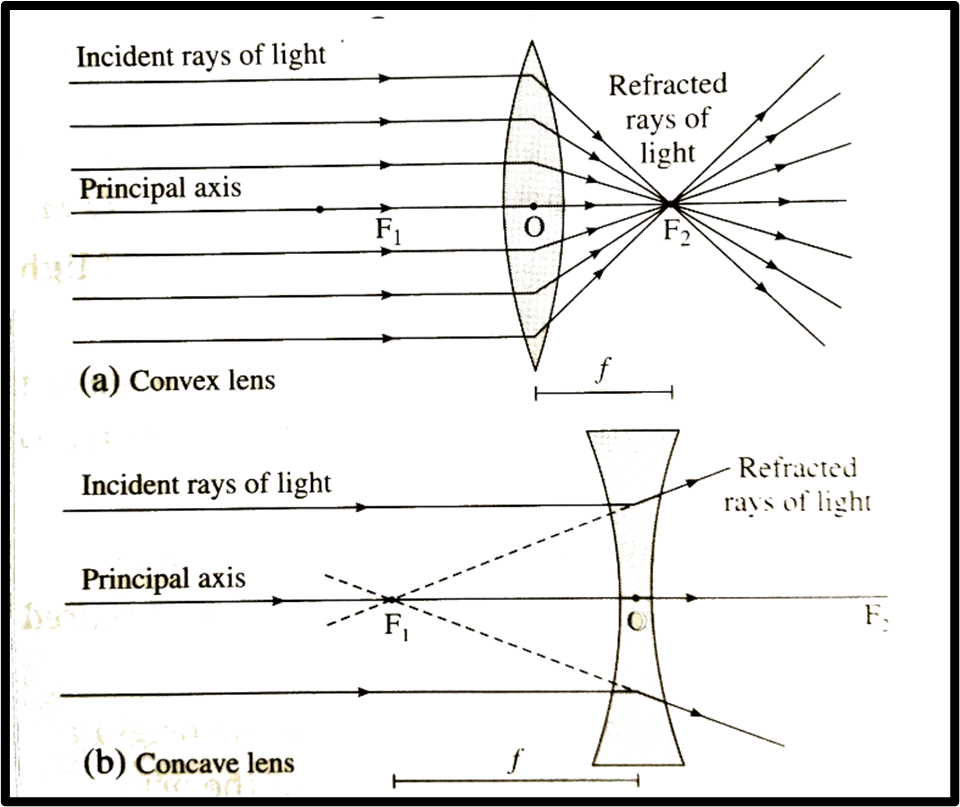
F₁, F₂: Principal foci of the lens, f: Focal length of the lens

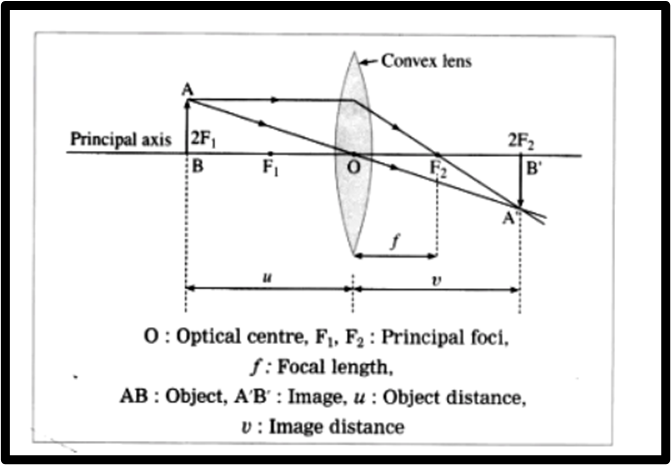
Question 3. At which position will you keep an object in front of a convex lens so as to get a real image of the same size as the object? Draw a figure.

Answer: At 2F1.

Question 4.

Give scientific reasons:

a. A simple microscope is used for watch repairs.

1. When an object is positioned within the focal length of a magnifying glass or simple microscope (convex lens), a larger and upright image appears on the same side of the lens as the object.
2. By changing the distance between the object and the lens, the image can be brought into focus at the closest point of clear vision. As a result, a watch repairer can observe the minute components of a watch more distinctly with the assistance of a magnifying glass (a simple microscope) compared to the naked eye, without straining the eyes. Therefore, watch repairers utilize a magnifying glass (a simple microscope) during the watch repair process.

b. One can sense colours only in bright light.

Answer. (1) The eye’s retina consists of numerous light-sensitive cells. Rod-shaped cells detect light intensity, while cone-shaped cells detect different colors.

(2) Cone-shaped cells are not sensitive to dim light and only operate effectively in bright light. Therefore, color perception is limited to well-lit conditions.

b. One can sense colours only in bright light.

(1) The eye’s retina consists of numerous light-sensitive cells. Rod-shaped cells detect light intensity, while cone-shaped cells detect different colors.

(2) Cone-shaped cells are not sensitive to dim light and only operate effectively in bright light. Therefore, color perception is limited to well-lit conditions.

c. We cannot clearly see an object kept at a distance less than 25 cm from the eye.

Answer. (1) As we focus on a nearby object, the eye lens becomes rounder and its focal length decreases, resulting in a sharp image on the retina.

(2) The eye lens has a minimum focal length limit, preventing clear vision of objects within 25 cm of the eye.

Question 5. Explain the working of an astronomical telescope using refraction of light.

Answer: The construction of a refracting telescope involves two convex lenses known as the objective lens (pointed toward the object) and the eyepiece (pointed toward the eye). The focal length and diameter of the objective lens are greater than those of the eyepiece. The objective lens is placed at one end of a long metal tube.

Within this metal tube, a smaller diameter tube is inserted, with the eyepiece placed at the outer end of the smaller tube. By adjusting the distance between the eyepiece and the objective lens using a screw and sliding the tube with the eyepiece, the setup can be modified. The principal axes of the objective lens and the eyepiece align along the same line, with the telescope typically mounted on a stand.

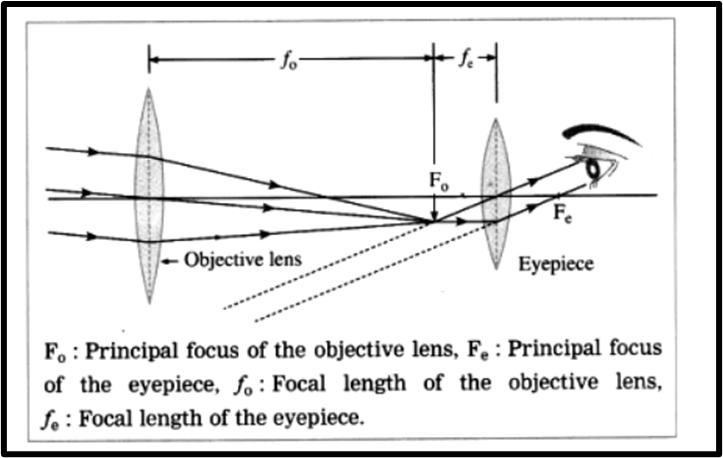
When the distant object is in focus, light rays from it pass through the large objective lens, creating a real, inverted, and smaller image. The eyepiece is then adjusted to magnify this image, which is viewed as virtual and enlarged by the observer.

Question 6.

Distinguish between the following:

a. Farsightedness (Hypermetropia) and Near sightedness (Myopia).

Answer. Farsightedness:

1. Hypermetropia is a condition where the eye can see things far away clearly but has difficulty seeing nearby objects.
2. In hypermetropia, the image of a close object is focused behind the retina.
3. This issue can be fixed by using a convex lens with the right strength.

Near sightedness:

1. Myopia is a vision condition where the eye can see close objects clearly but struggles to see distant objects sharply.
2. The distant object’s image is focused in front of the retina in such cases.
3. This issue can be fixed by using the right power concave lens.

b. concave lens and convex lens.

Concave lens

1. A concave lens curves inward on its surfaces,
2. with greater thickness at the edges than in the middle,
3. resulting in the formation of solely virtual and smaller images.

Convex lens:

1. A convex lens bulges outward on its surfaces, being thicker at the centre than at the edges.
2. This type of lens is capable of producing both real and virtual images,
3. which may appear magnified, reduced, or the same size as the object depending on the object’s placement.

Question 7. What is the function of the iris and the muscles connected to the lens in the human eye?

Answer. In bright light, the iris muscles expand to shrink the pupil, while in dim light, the iris muscles contract to enlarge the pupil. This mechanism allows the iris to manage pupil size and control the entry of light into the eye.

Observing a distant object result in the relaxation of the ciliary muscles, causing the eye lens to flatten and increase its focal length. Consequently, a clear image of the distant object is produced on the retina, allowing for improved visibility

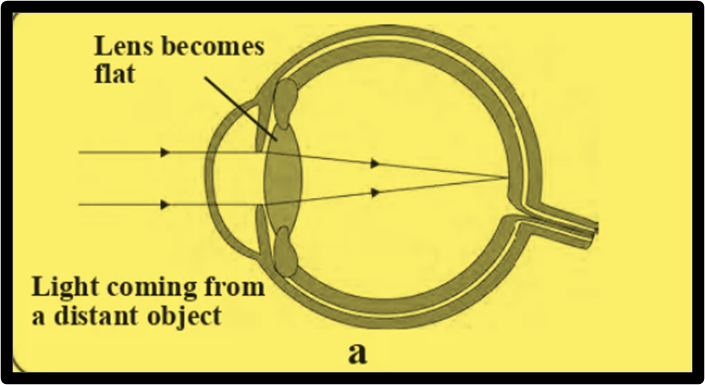
formation of an image of a distant object

When an object is closer to the eye, the ciliary muscles contract to increase the curvature of the eye lens. As a result, the eye lens becomes more rounded, reducing its focal length. This allows a clear image of the nearby object to be formed on the retina, enabling clear vision of close objects

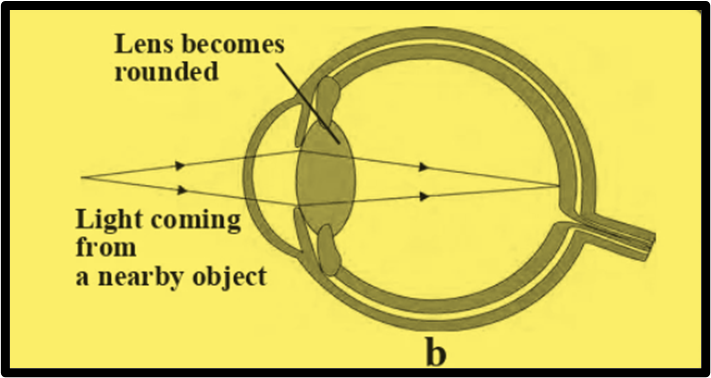
formation of an image of a nearby object

Question8.Doctor has prescribed a lens having I power + 1.5 D. What will be the focal length of the lens? What is the type of the lens and what must be the defect of vision?

Answer.The focal length (f) tells us how far away the lens needs to be from an object to focus the light properly. We can find it using a simple formula:

f = 1 / P

where f is the focal length and P is the power of the lens (in Diopters).

Calculating for this lens:

P = +1.5 D (given)

f = 1 / (+1.5 D)

f ≈ 1 / 1.5 m^-1 ≈ 0.667 meters ≈ 67 centimeters

P is positive. This shows that the lens is convex. The defect of vision is farsightedness (hypermetropia).

ii. 5 cm high object is placed at a distance of 25 cm from a converging lens of focal length of 10 cm. Determine the position, size and type of the image.

Solution.  Plug in the known values: 1/10 = 1/-25 + 1/v

Solve for v: v ≈ 16.67 cm (rounded to two decimal places)

Step 2: Find the image height (h2):

Now that you know v, you can use another formula: h2 = h1 * v / u

Plug in the values: h2 = 5 cm * 16.67 cm / -25 cm

Solve for h2: h2 ≈ -3.33 cm (rounded to two decimal places)

(iii) The image is real, inverted and smaller than the object.

iii. Three lenses having powers 2, 2.5 and 1.7 D are kept touching in a row. What is the total power of the lens combination?

• P = P1 + P2 + P3
• P = 2 D + 2.5 D + 1.7 D
• P = 6.2 D

iv. An object kept 60 cm from a lens gives a virtual image 20 cm in front of the lens. What is the focal length of the lens? Is it a converging lens or diverging lens?

Solution:

u = -60 cm: This is the object distance, meaning the object is 60 cm to the left of the lens (negative sign indicates that).

v = -20 cm: This is the image distance, meaning the image is 20 cm to the right of the lens (negative sign indicates that).

f = ?: This is the focal length we need to find.

The lens formula relates the object distance (u), image distance (v), and focal length (f) of a lens system:

1/f = 1/v – 1/u  = 1/ -20 – 1/ -60

= – (1/ -20 cm  – 1/ -60 cm)

Lcm  of  20 and  60 is  60

= – (3 -1 / 60 )

= -2/60

= -1/30

∴ The focal length of the lens, f = – 30 cm. As f is negative, it is a diverging lens.