Question1.
Fill in the blanks and explain the completed statements:
a. Refractive index depends on the…………. of light.
Answer: Refractive index depends on the velocity of light.
It is an experimental fact. (This is an established observation with no need for further clarification.)
b. The change in…………of light rays while going from one medium to another is called refraction.
Answer: The change in the direction of propagation of light rays while going from one medium to another is called refraction. Refraction is defined as the phenomenon that occurs when a light ray moves diagonally from one medium to another.
Question 2. Prove the following statements:
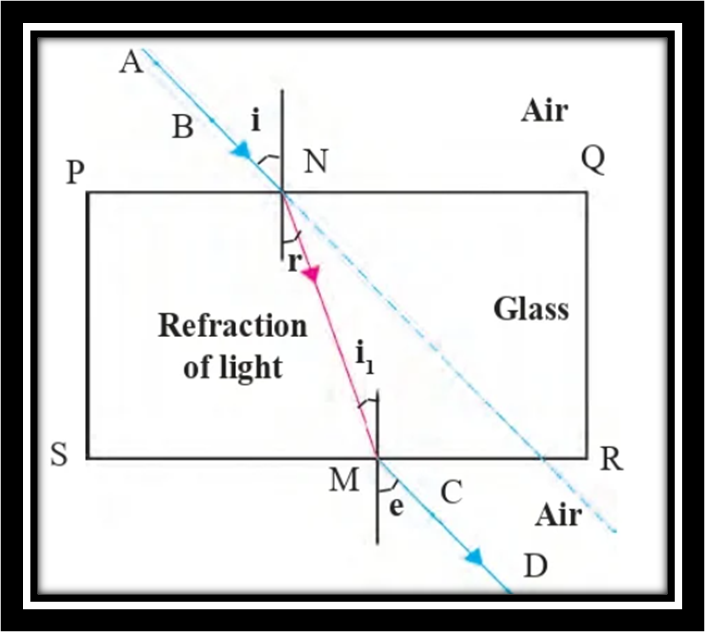
a. If the angle of incidence and angle of emergence of a light ray falling on a glass slab are i and e respectively, prove that i = e.
Answer. Consider a light ray passing through a glass slab as shown in the diagram below. The incident ray enters the glass slab at an angle of incidence (i) and is then refracted, changing its direction. The refracted ray (NM) exits the glass slab at an angle of emergence (e).
We can establish a relationship between the angles of incidence and emergence using Snell’s law of refraction, which states that:
where:
- n1 is the refractive index of the medium from which the light ray is entering (in this case, air)
- n2 is the refractive index of the medium through which the light ray is passing (in this case, the glass slab)
- i is the angle of incidence
- r is the angle of refraction
Since the incident ray (SR) is parallel to the refracted ray (NM), we have:
i1 = r
Substituting this into Snell’s law, we get:
n1 sin i = n2 sin i1
Rearranging and dividing both sides by sin i, we obtain:
n1 = n2
We can establish a relationship between the angles of incidence and emergence using Snell’s law of refraction, which states that:
n1 sin i = n2 sin r
where:
- n1 is the refractive index of the medium from which the light ray is entering (in this case, air)
- n2 is the refractive index of the medium through which the light ray is passing (in this case, the glass slab)
- i is the angle of incidence
- r is the angle of refraction
Since the incident ray (SR) is parallel to the refracted ray (NM), we have:
i1 = r
Substituting this into Snell’s law, we get:
n1 sin i = n2 sin i1
Rearranging and dividing both sides by sin i, we obtain:
n1 = n2
This means that the refractive index of air (n1) is equal to the refractive index of the glass slab (n2), which is not true. Therefore, our initial assumption that r = i1 must be incorrect.
To correct our assumption, we can consider the angle of refraction at the second surface of the glass slab. Since the refracted ray (NM) is entering from a denser medium (glass) to a less dense medium (air), it will bend away from the normal. Let’s denote this angle of refraction as i2.
Applying Snell’s law at the second surface, we have
n2 sin i2 = n1 sin e
Substituting n2 = n1 from our previous analysis, we get:
sin i2 = sin e
Since the refracted ray (NM) is also parallel to the emergent ray (PQ), we have:
i2 = e
Therefore, we can conclude that the angle of incidence (i) is equal to the angle of emergence (e) for a light ray passing through a glass slab. This implies that the light ray retraces its path within the glass slab, emerging parallel to its incident direction.
b. A rainbow is the combined effect of the refraction, dispersion, and total internal reflection of light
Answer: The rainbow forms in the sky due to a combination of sunlight being refracted, dispersed, internally reflected, and refracted again by water droplets in the atmosphere following rainfall. Typically, only violet and red colors are visible, with the other five colors present in between.
Sunlight comprises seven colors: violet, indigo, blue, green, yellow, orange, and red. After rain ceases, the atmosphere contains numerous water droplets. When sunlight hits a water droplet, it undergoes refraction and dispersion as it moves from air to water, internal reflection within the droplet, and refraction as it exits from water to air.
Water has varying refractive indexes for different colors, with the highest for violet and the lowest for red, causing light to disperse into different colors as it transitions from air to water.
The collective effect of numerous water droplets, behaving like small prisms, results in the creation of a rainbow, with red on the outer edge and violet on the inner side, while the other five colors are in between. Rainbows are visible when the sun is positioned behind the observer with water droplets in the foreground.
Question 3. Mark the correct answer in the following questions:
A. What is the reason for the twinkling of stars?
(i) Explosions occurring in stars from time to time
(ii) Absorption of light in the earth’s atmosphere
(iii) Motion of stars
(iv) Changing refractive index of the atmospheric gases
Answer: Changing refractive index of the atmospheric gases.
B. We can see the Sun even when it is a little below the horizon because of
(i) reflection of light
(ii) refraction of light
(iii) dispersion of light
(iv) absorption of light
Answer: refraction of light
C. If the refractive index of glass with respect to air is 3/2, what is the refractive index of air with respect to glass?
(i) 1/2
(ii) 3
(iii) 1/3
(iv) 2/3
Answer.2/3 The refractive index of air concerning glass is 2/3,
Question4. Solve the following Examples.
a. If the speed of light in a medium is 1.5 × 108 m/s, what is the absolute refractive index of the medium? (Practice Activity Sheet – 1 and 4)
Solution. The absolute refractive index of a medium tells us how much slower light travels in that medium compared to a vacuum. We can find it using the following formula:
Absolute refractive index (n) = Speed of light in vacuum (c) / Speed of light in the medium (v)
Where:
c = Speed of light in vacuum ≈ 3 × 10^8 m/s
v = Speed of light in the medium = 1.5 × 10^8 m/s (given in the question)
Now, plug the values into the formula:
n = (3 × 10^8 m/s) / (1.5 × 10^8 m/s)
n = 2
Therefore, the absolute refractive index of the medium is 2. This means that light travels half as fast in this medium compared to a vacuum.
b.If the absolute refractive indices of glass and water are 3/2 and 4/3 respectively, what is the refractive index of glass concerning water?
Solution: Given: Refractive index of glass (n_glass) = 3/2
Refractive index of water (n_water) = 4/3
Refractive index represents the relative speed of light in two materials.
A higher index indicates slower light compared to a lower index.
Calculation:
To find the refractive index of glass with respect to water, we simply divide their individual refractive indices: n_glass / n_water = (3/2) / (4/3)
Simplify:Multiply both top and bottom by 3: n_glass / n_water = (9/6) / (12/6)
Simplify further: n_glass / n_water = 9/8
Therefore, the refractive index of glass with respect to water is 9/8. This means that light travels 8/9 times faster in glass compared to water.