1. A sum of money invested at compound interest of 8% p.a. compounded annually, amounts to ₹7290 in two years. Find the sum invested.
Solution:
We know the formula: Amount = P (1 + R/100)^T
Here, Amount = ₹7290, R = 8%, T = 2 years. We need to find P.
7290 = P × (1 + 8/100)²
7290 = P × (1.08)²
7290 = P × 1.1664
P = 7290 ÷ 1.1664
P = ₹6,250
Answer: The sum invested was ₹6,250.
2. An investment at the rate of 18% p.a. compounded annually amounts to ₹4177.20 in two years. What was the sum invested?
Solution:
Amount = ₹4177.20, R = 18%, T = 2 years.
4177.20 = P × (1 + 18/100)²
4177.20 = P × (1.18)²
4177.20 = P × 1.3924
P = 4177.20 ÷ 1.3924
P = ₹3,000
Answer: The sum invested was ₹3,000.
3. If the amount after 3 years at the rate of 12½% per annum compounded annually is ₹10,935, find the principal.
Solution:
Amount = ₹10,935, R = 12.5%, T = 3 years.
10935 = P × (1 + 12.5/100)³
10935 = P × (1.125)³
10935 = P × 1.423828125
P = 10935 ÷ 1.423828125
P = ₹7,680
Answer: The principal was ₹7,680.
4. If a sum of ₹40,000 at compound interest of 5% p.a. amounts to ₹44,100, find the time for which the money was invested.
Solution:
P = ₹40,000, Amount = ₹44,100, R = 5%.
We use the formula: Amount = P (1 + R/100)^T
44100 = 40000 × (1 + 5/100)^T
44100 / 40000 = (1.05)^T
1.1025 = (1.05)^T
Notice that (1.05)² = 1.1025.
So, T = 2 years.
Answer: The money was invested for 2 years.
5. In how many years will ₹6750 amount to ₹8192 at 6⅔% p.a. compounded annually?
Solution:
P = ₹6750, Amount = ₹8192, R = 6⅔% = 20/3%.
8192 = 6750 × (1 + (20/3)/100)^T
8192 / 6750 = (1 + 1/15)^T
8192 / 6750 = (16/15)^T
1.213629… = (16/15)^T
Notice that (16/15)³ = 4096 / 3375 = 1.213629…
So, T = 3 years.
Answer: It will take 3 years.
6. In how many years will ₹2000 amount to ₹2163.20 at 4% p.a. compounded annually?
Solution:
P = ₹2000, Amount = ₹2163.20, R = 4%.
2163.20 = 2000 × (1 + 4/100)^T
2163.20 / 2000 = (1.04)^T
1.0816 = (1.04)^T
Notice that (1.04)² = 1.0816.
So, T = 2 years.
Answer: It will take 2 years.
7. Find the difference between simple interest and compound interest on ₹2400 for 2 years at 5% per annum compounded annually.
Solution:
Step 1: Calculate Simple Interest (SI)
SI = (P × R × T) / 100 = (2400 × 5 × 2) / 100 = ₹240
Step 2: Calculate Compound Interest (CI)
First, find the Amount.
A = P (1 + R/100)^T = 2400 × (1.05)² = 2400 × 1.1025 = ₹2,646
CI = A – P = 2646 – 2400 = ₹246
Step 3: Find the Difference
Difference = CI – SI = 246 – 240 = ₹6
Answer: The difference is ₹6.
8. Find the difference between simple interest and compound interest on ₹6400 for 2 years at 6¼% p.a. compounded annually.
Solution:
Calculate Simple Interest (SI)
R = 6¼% = 6.25%
SI = (6400 × 6.25 × 2) / 100 = (80000) / 100 = ₹800
Calculate Compound Interest (CI)
A = 6400 × (1 + 6.25/100)² = 6400 × (1.0625)² = 6400 × 1.12890625 = ₹7,225
CI = A – P = 7225 – 6400 = ₹825
Find the Difference
Difference = CI – SI = 825 – 800 = ₹25
Answer: The difference is ₹25.
9. The CI for a sum of money for 2 years at the rate of 10% per annum compounded annually is ₹315. Find the simple interest for the same sum for the same period at the same rate.
Solution:
- Compound Interest (CI) for 2 years at 10% p.a. is given by:
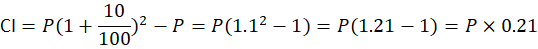
- Given CI = ₹315, so:
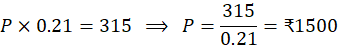
- Simple Interest (SI) for the same sum, rate, and time:
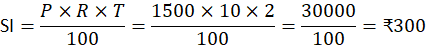
Answer: The simple interest is ₹300.
10. The difference between SI and CI of a certain sum of money is ₹48 at 20% p.a. for 2 years. Find principal. (Hint: Assume the principal as ₹100.)
Solution:
- The difference between CI and SI for 2 years is given by:
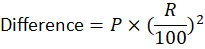
- Substituting R = 20%:
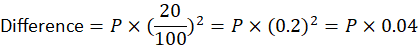
- Given difference = ₹48, so:
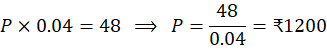
- Using the hint (assuming P = ₹100):
- SI for 2 years =
- CI for 2 years =
- Difference = ₹44 – ₹40 = ₹4
- Since actual difference is ₹48, scaling factor =
, so principal =
Answer: The principal is ₹1200.
- SI for 2 years =
11. In how many years will a sum of ₹6400 compounded semi-annually at 5% p.a. amount to ₹6560?
Solution:
- Compounded semi-annually, so rate per half-year =
- Let the number of half-years be
. Then:
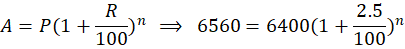
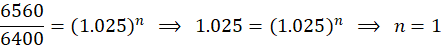
- Since
half-year, the time in years is
years.
Answer: The time required is 0.5 years (or 6 months).
12. What sum invested for years compounded half-yearly at the rate of 4% p.a. amounts to ₹1,32,651?
Solution:
- Time =
years = 3 half-years
- Rate per half-year =
- Let the principal be
. Then:
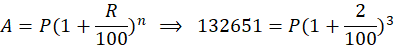
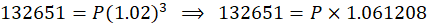
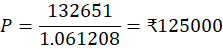
Answer: The sum invested is ₹125,000.